PREMIER Nesting and Pseudoreplication
Background
Biologists determine experimental effects by perturbing biological entities or units. When done appropriately, independent replication contributes to the sample size (N) and forms the basis of statistical inference. Pseudoreplication artificially inflates the sample size, and thus the evidence for a scientific claim, resulting in false positives [[1]]. The term `replication' has several related meanings, and here it refers to the classic statistical definition of an intervention or treatment applied to multiple biological entities i.e. experimental units (EUs). It does not refer to researchers trying to reproduce or replicate their own or others' results [1].
There are two types of replication:
- The first is replication that increases the sample size (N) and thus contributes to testing an experimental hypothesis. It is called true, genuine, or absolute replication.
- The second type is replication that does not increase the sample size and is called pseudoreplication. Confusing pseudoreplication for genuine replication artificially inflates the sample size, thereby inflating the apparent evidence supporting a scientific claim, and contributes to irreproducible results.
Optimization of experimental designs nearly always concerns collection of more truly independent observations, rather than more observations from one research object [2].
Tasks / Actions
Nesting refers to statistical term "nested data". Those occur when the observation of a dataset can be assigned to units of superordinate hierarchy. A leveled analysis is necessary to reveal these relationships. In biomedicine, nested data present a problem when they are counted as the true sample size. The following paragraphs are designed to prevent such pitfalls already at the stage of the study design.
Nested designs are designs in which multiple observations or measurements are collected in each research object (for example, animal, tissue sample or neuron/cell). Consider the following fictive, yet representative, research results. “The channel blocker significantly affected Ca2+ signals (n = 120 regions of interest (ROI) from 10 cells, P < 0.01).” “The number of vesicles docked at the active zone was smaller in presynaptic buttons in mutant neurons than in WT neurons (n = 20 and 25 synapses each from 3 neurons for mutant and WT, P < 0.01).” Both statements concern experimental designs involving nested (or clustered) data.
These nested designs are particularly common to neuroscience, as many research questions in neuroscience consider multiple layers of complexity: from protein complexes, synapses and neurons, to neuronal networks, connected systems in the brain and behavior. In such multiple layer–crossing designs, careful consideration of the issues that come with nesting is crucial to avoid incorrect inferences (2).
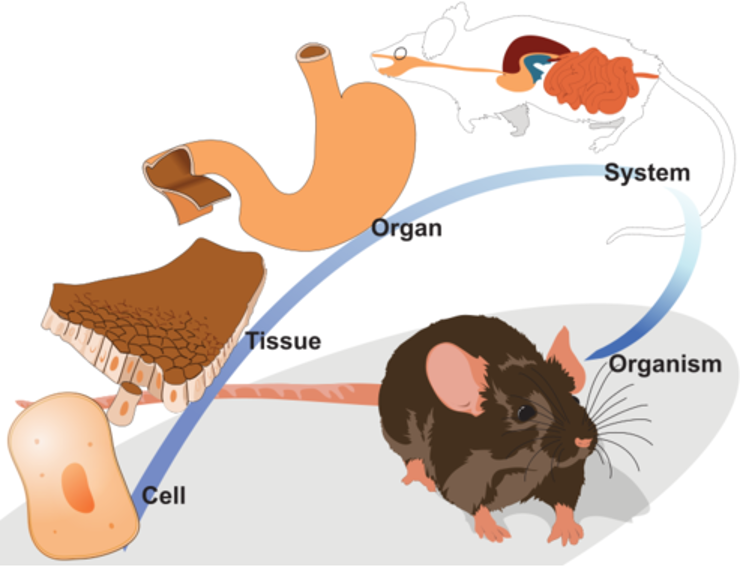
True or genuine replication increases the samples size (N) and contributes to testing an experimental hypothesis. Pseudoreplication artificially inflates the samples size, which leads to more false positive results. Problem: Often pseudoreplication is mistaken for genuine replication. The problem is are multiple layers of biological organization. (DNA-->RNA-->protein-->tissue-->organ-->organism)
Properties at one level of biological organization tend to be influenced by those above. In the same organism, two cells in same tissue tend to be more alike, then cells between different tissues. Research hypothesis, experimental manipulation and measurement can be assigned to different levels of biological organization.
Each study contains replication that is relevant to the hypothesis being tested. Therefore, it is important to define:
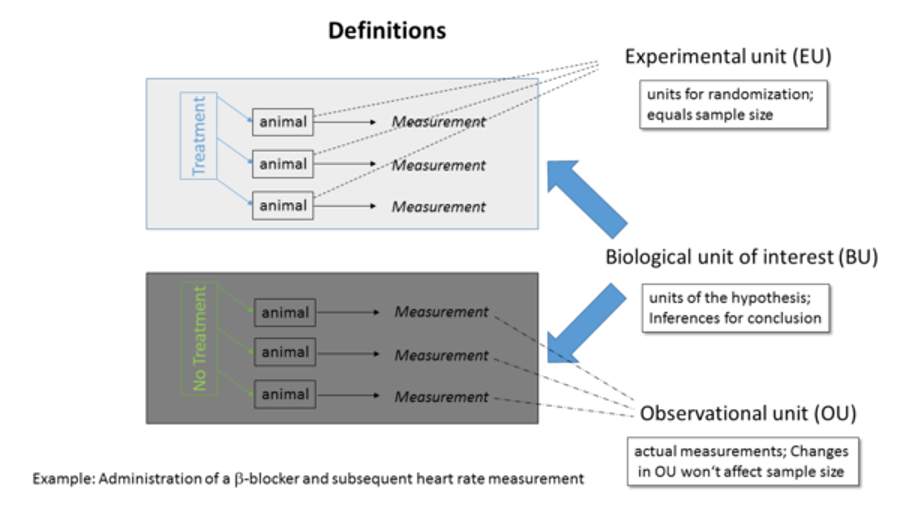
- Biological Unit (BU) of interest which is the entity about which inferences are made. The purpose of an experiment is to test a hypothesis, estimate a property, or draw a conclusion about BUs.
- Experimental Unit (EU) is the entity randomly and independently assigned to the experimental conditions. EUs must not influence each other, especially on the measured outcome variable. The sample size (N) is equal to the number of EUs.
Observational Unit (OU) corresponds to the entity on which the actual measurements are made, which may be different from the EUs and BUs of interest. Increasing the number of OUs does not increase the sample size.
In every study design the conditions must be tested to determine whether the OU is the experimental unit or if there is another superordinate hierarchy. In following, the hierarchical characteristics for different experimental types and setups are laid out.
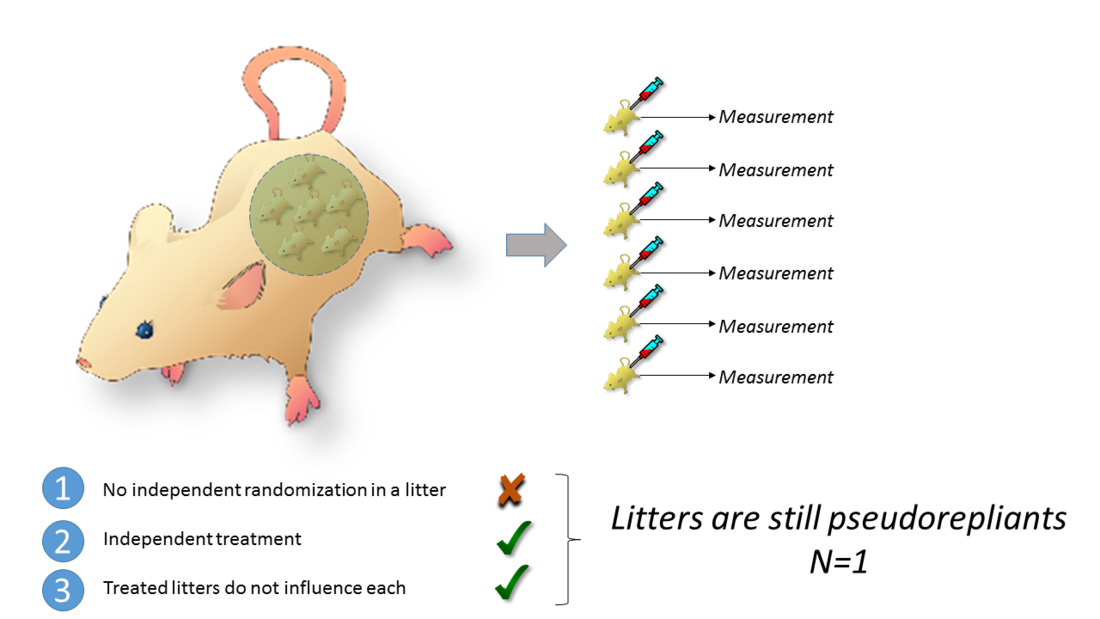
If treatments are randomly and independently applied to an entity other than the individual animal (e.g. pregnant females), then the sample size is not the number of animals. Offspring rarely meet the criteria for genuine replications.
A possibility is to apply treatment after offspring are born. They are then randomized by litter to the treatment groups. The problem with this design is that the variable litter is nested under the variable group
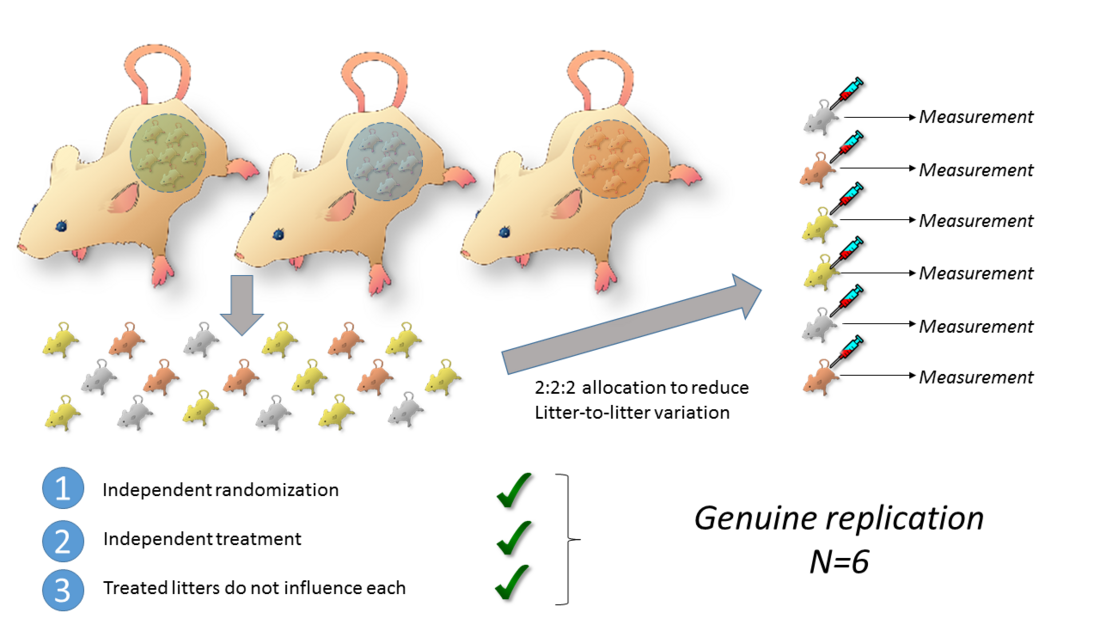
A solution can be a crossed arrangement which crossed litters and treatment groups: Individual animals are randomized to the treatment condition which removes the litter-to-litter variation
This applies to all recognizable subgroups, such as transgenic and wild-type mice.
If a treatment is applied cage-wise, then cages are the experimental unit. Only when the treatment is applied independently, animal act as EU.
In many animal experiments, the condition for genuine replication (treated animals do not influence each other) is often overlooked. In reality mandatory group housing violates this condition, because animals in the same cage influence each other on many relevant variables, from behavior to microbiome. Even if the first two criteria for genuine replication are met, mutual influence of animals in the same cage may render them unsuitable to be an EU. A solution would be one animal housing per cage which is often not possible for animal-ethical reasons. A compromise could be to house 2 animals maximum per cage (which is then the EU) for all animals of the study.
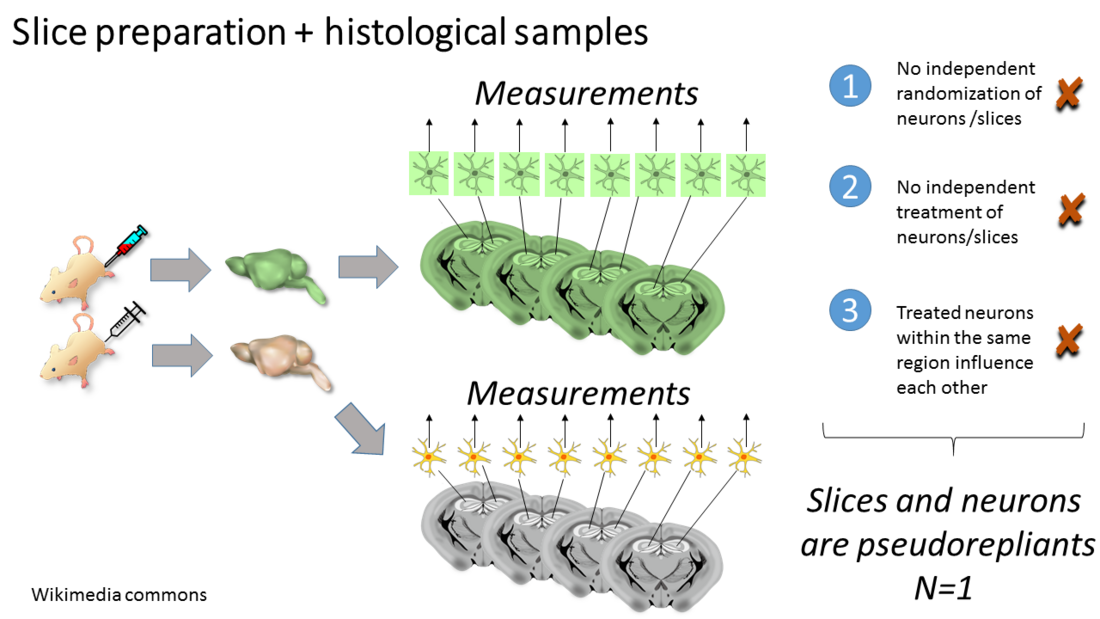
For some experiments, animals are randomized to treatment conditions and an intervention is applied to the animals. Then an organ or body part is examined, usually postmortem. Because of the large size or diversity of the body parts, multiple histological sections, neurons per section, spines per neuron are counted. All of these OU have been randomized together (I), the treatment is applied simultaneously (II) and treated neurons and spines within an area of interest may influence each other (III). Therefore animals are the EU in this case.
If the body part is removed first, treatment is applied, and then observations are made, multiple body parts per animal can used , especially the one that come in pairs (brain hemispheres, kidneys, lungs, testes, ovaries) can be used and individually randomized and treated. This approach can also reduce also the number of animals in a study. Sample size is then the body part but it is strongly advised to use multiple animals to establish the robustness of the investigated effect.
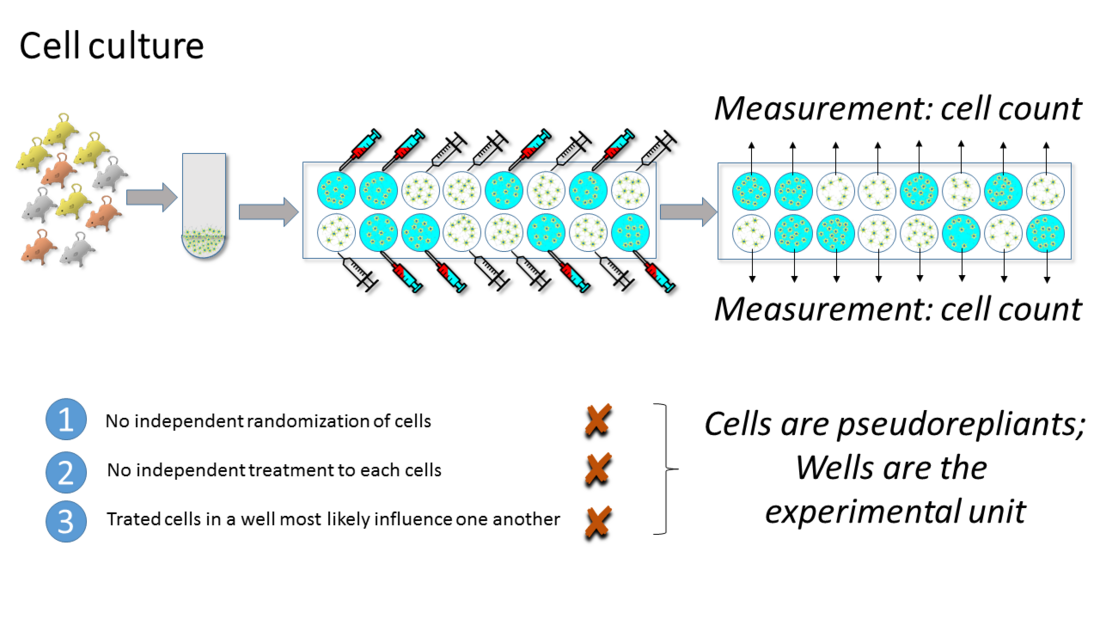
In cell culture experiments cells are often both, the BU and OU, but rarely the true EU.
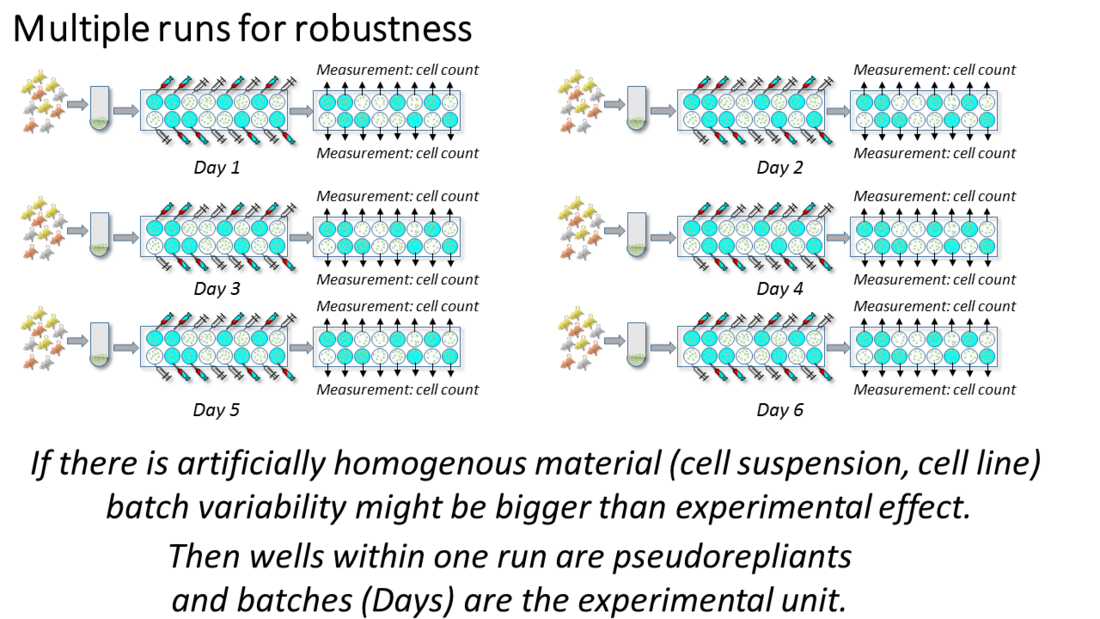
There is a lot of batch-to-batch variability in cell culture experiments because the experimental material needs to be created for every experiment. For this reason such in-vitro experiments are usually repeated on multiple days, and the number of wells, aliquots, or culture dishes within a given day are treated as subsamples. In order to test whether a phenomenon is robust, multiple replications of the entire experimental run or protocol are required. This cannot be done on a one day setup using a large number of samples. Multiple repetitions provide an estimate of the consistency of the effects across different experimental runs on different days
- Lazic SE, Clarke-Williams CJ, Munafò MR. What exactly is 'N' in cell culture and animal experiments?http://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.2005282 PLoS Biol. 2018 Apr 4;16(4):e2005282. doi: 10.1371/journal.pbio.2005282. PMID: 29617358;
- Aarts E, Verhage M, Veenvliet JV, Dolan CV, van der Sluis S. A solution to dependency: using multilevel analysis to accommodate nested data. Nat Neurosci. 2014 Apr;17(4):491-6. doi: 10.1038/nn.3648. Epub 2014 Mar 26. PMID: 24671065.